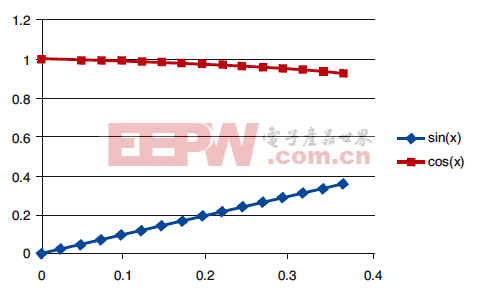
图 2 — d 值的正弦与余弦表，范围介于0到360/16度之间

　　实际上， 我们在每个表格中都使用了1 , 0 2 4 个值。X的最小值为360/1024=0.3515625 度。d 的所有值都将小于等于该值。该方法可以减少存储的占用，因为完整的查找表需要 4,096个条目(每条目 4 个字节)。

　　使用这种方案，我们能够实现的自变量总体精度为：

　　360/(1024*1024) = 0,000343 degree

　　而且这个精度非常好。计算充分利用了MicroBlaze FPU。

　　真正的计算会占用一些时钟周期，具体来说，需要进行两次fmul运算和一次fadd运算。不过，我们还需要进行一些其它计算。首先，我们必须把自变量 xi拆分成两个值，对应x和d;然后，我们将这两个值从表格中读出;最后，我们必须使用新的算法才能计算结果。

　　我们在软件中实现算法并对其进行测试时，我们耗用的时钟周期总数为6,520个。

　　为了进一步提高分辨率，我们可以使用下列的象限关系：

　　第一象限

　　sin(x) = sin(x)

　　第二象限

　　sin(x) = sin(π - x)

　　第三象限

　　sin(x) = -sin(π + x)

　　第四象限：

　　sin(x) = -sin(2* π - x)

　　这在保持表格大小不变的同时还可将总体分辨率提高4倍。另一方面，我们需要进行更多的计算才能找出我们必须进行计算的象限是哪一个。仍然需要改进算法或缩小表格的大小(缩小四分之几)。我们还没有进行到这一步。

　　步骤三：优化算法

　　由于我们的解决方案到目前为止，速度还不能满足我们客户的需要，因而我们需要稍做算法优化，不过仍然完全采用运行在 MicroBlaze 处理器上的软件。这是一种简单的优化方案，不过会降低部分精度。因此，我们创建了软件模型(在PC上运行以提升运行速度)以运行所有可能的值，同时使用 sin()计算出的原始双精度值与使用我们的软件算法计算出的正弦值进行比较。我们决定在标准的PC上运行算法，因为在MicroBlaze上进行比较和计算需要花较长的时间(注意，我们的MicroBlaze运行速度远低于PC)。

　　现在我们开始优化计算以获得正弦值：

　　sin(x+d) = sin(x)*cos(d) +cos(x)*sin(d)

　　由于在每个表格中我们都使用了1,024个值，这意味着d始终小于360度/1,024个步进，即：

　　cos(2* π /1024) = 0.99998

　　而且该值约等于1.0。对较小的d值，适用下列等式：

　　cos(d) = ~1.0

　　这样可以将我们的公式简化为如下等式：

　　sin(x+d) = sin(x) + cos(x)*sin(d)

　　在我们在MicroBlaze上实现新等式之前，我们使用PC模式对新等式的精度进行了检验，发现最大误差仍然低于我们客户的目标。

　　现在我们将该算法当作软件算法在MicroBlaze上实现，仍然使用每张带有1,024个条目的表。新的算法只需要三个表，比之前的实现方案少一个。这样既节省了存储空间，也为更多的计算留出了时间。

　　我们在我们的硬件上测量了算法。一次正弦计算需要6,180个周期。

　　步骤四：进一步优化

　　另一种看似可行的优化方式是转换正弦计算的浮点值，并在此使用整数自变量。我们使用的算法使我们能够创建~1E6 个不同的值 (1,024*1,024)。整数自变量足以处理这个数量的值。

　　这种优化方式使我们能够使用简单得多的计算来将 xi 值拆分为 x 和 d。拆分只是一种简单的“与”运算加上部分10 位的移位。我们参数角的上10位是xi，下10位是 d。

　　我们再次在PC上创建了一个软件模型，并对其进行检验，然后在MicroBlaze处理器系统上实现模型，这需要5,460个周期才能完成一次正弦计算。

　　步骤五：考虑硬件实现

　　虽然与数学库的原始计算相比，算法的速度有了明显的改善，但客户需要的是速度快得多的实现。不过前文所述的最后一步给我们提供了一种能够轻松转向硬件实现的方法。

　　这种实现方法需要某些用于拆分 xi值的运算。要在硬件中做到这一点，只需将所需的位进行连接即可。然后我们需要三个表;我们使用以我们的PC模型计算出的预定义值推导出ROM，然后将其转入IP的VHDL代码中。该IP能够一次读取所有三个表，从而能够再度节省时间。最后，我们需要进行一次浮点MUL和一次浮点ADD运算。

　　对于该任务，我们发现用于浮点运算的CORE GeneratorTM模块非常适合。

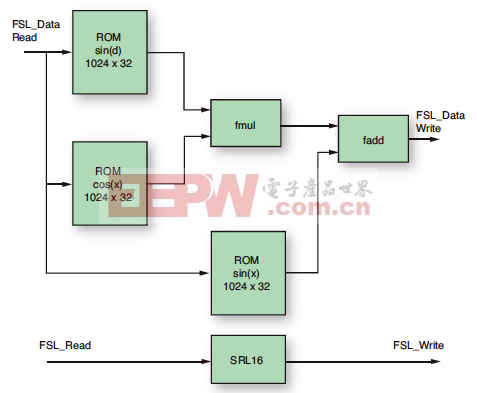
　　图 3 — 无流水线功能的加速器 IP