算法设计
频域自适应干扰抵消(AIC)模块利用了频域实现的LMS算法[2,3]。该算法通过1/2重叠保留法的快速傅立叶变换(FFT)，在频域以直接相乘的计算方式实现快速相关和快速卷积[4]。算法基本框图如图3，其中A点为被干扰的信号，B为反馈链路的信号，C点为干扰被抵消后的输出。主要包括以下循环执行的操作流程，其中k表示第个k数据块：
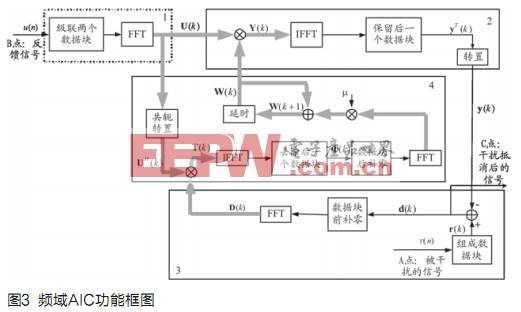
(1)对自适应滤波器的M个频域抽头系数W(k)作初始化设置;
(2)将滤波器的时域连续输入信号u(n)每个M组成一个块，然后级联两个数据块做N点离散快速傅立叶变换，使其转换为频域信号U(k)，并将此信号用作自适应滤波器的输入;其中N是该滤波器抽头个数M的2倍，即N=2M;
(3)将U(k)通过滤波器得到输出信号Y(k)，然后进行快速傅立叶逆变换(IFFT)处理，使其转换为时域信号y(k)，作为干扰的估计值;
(4)计算被干扰信号r(k)和y(k)的差值，即为干扰抵消后的信号d(k);再产生该期望信号的频域值D(k)为下一次滤波器抽头系数迭代所使用;
(5)利用频域信号进行最小均方误差LMS计算，即根据D(k)和U(k)对W(k)进行更新，并将此更新值返回到步骤(2)中使用。跳转到步骤(2)进行反复迭代，直至干扰被抵消。
与传统的时域LMS算法相比，利用频域LMS算法可以降低计算复杂度。假设输入为实信号，滤波器抽头个数为。可以得到，频域LMS和时域LMS的计算复杂度之比为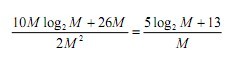
。实际中，干扰在空中传输的时延会比反馈信号的时延大得多，这时需要较大的抽头个数才能抵消干扰。假设M=1024，则频域LMS算法可以比时域LMS算法的速度提高大约16倍。为简化起见，在本文档中取M=64，利用频域LMS算法，在计算量角度大约可以比时域LMS算法快1.5倍。
