摘 要: 从相关时差估计的基本原理出发,提出了一种并行时域相关结构,基于这种并行结构设计实现了一种简单高效的时差估计器。与传统频域相关时差估计器相比,这种时差估计器的主要优点是提高了运算效率,运算周期大为缩短,可以满足实时高精度时差估计的需求,同时结构简单,硬件资源开销小,易于设计实现。实际测试结果验证了上述结论。
关键词:无源定位;到达时间差(TDOA);互相关;并行结构
无源时差定位系统利用多个观察站接收目标辐射源的信号,通过估计各个观察站接收信号之间的到达时间差,完成对目标辐射源的定位,具有作用距离远、隐蔽性强、定位精度高等优点。通常是通过对各个接收站的中频信号进行互相关,比较接收信号之间的相似性来得到高精度的到达时间差估计结果[1-2]。
对于无源时差定位中所处理的雷达信号,一般可以检测出脉冲的到达时间,也就大体知道了到达时间差[3],从而可通过控制相关序列的采样时机,只求解相关函数相关峰附近的相关值就可获得时差信息。而相关函数的计算一般利用FFT/IFFT快速算法进行频域相关,频域相关会同时计算全部相关信息,在已知粗略时差范围时效率并不高(对于长度为N的采样序列,用频域相关法估计时差需要进行3个2N点FFT/IFFT运算和2N次复数乘法),而且大点数FFT/IFFT的工程实现也非常困难,运算时间与硬件资源开销严重,不适于进行实时时差估计[4- 5]。
本文利用时域相关可只求解部分相关值的优势,设计实现了一种并行相关结构的时差估计器,大大缩减了运算时间,可以满足实时时差估计的需求,同时简化了硬件结构、降低了硬件开销与实现难度。
1 基本原理[6-8]
假设辐射源辐射的信号为实信号s(t),被两个接收机接收的信号分别为x(t)和y(t),具有不同的噪声和时间延迟,两信号可表示为:
由于信号与噪声互不相关,Rsn1=Rsn2=0,因此可得到:
若需±m(0mN)范围内的相关值,可以用2m+1个乘累加器并行计算来减小运算时间。不失一般性,以一个N=4,m=2的相关运算为例,将每个乘累加器所需进行的乘运算列于表1(clk表示乘周期)。
在工程实际中,中频采样后的数据一般存储于双口RAM或FIFO中,每个时钟沿最多可提供两个不同地址的数据。然而,由式(7)与表1看出,每个乘累加器每个周期所需的输入数据都不一致,要为这些累加器同时提供不同的输入数据几乎是不可能的,尤其是在时钟速率与采样位数都较高的情况下。

对乘累加器每个周期所进行的乘运算进行调整,如表2所示。从中可以发现:相关结果未发生变化;每个乘周期所有乘累加器的输入都相同;第i个乘累加器当前周期的x输入为第i-1个乘累加器上一乘周期的x输入。由此,可设计一种并行流水结构来避免多个乘累加器同时工作时对数据吞吐率的要求。
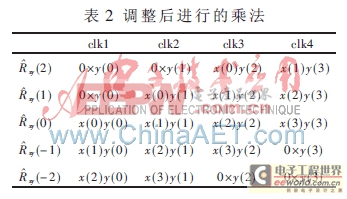
如图1所示,每个乘累加器的y输入相同,x输入则由上一个乘累加器的x输入经过一延迟寄存器得到,整个并行相关器每个周期只需读入两个新的输入数据,数据吞吐率得以大大降低。需注意的是,为了求得±m(0mN)范围内的相关值,需要对输入序列进行简单的调整,即在y输入序列之前和x输入序列之后各补m个零。实际上,只要对x与y输入序列做出补零或截取这样的调整,此结构可以求任意2m+1连续范围内的相关值。并且在数据输入完毕后,所有乘累加器同时输出各自的相关结果。
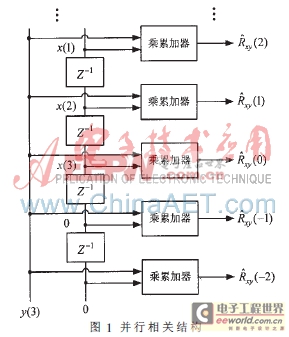
在实际进行设计时,上述流水结构依然面临难题。在乘累加器较多、时钟速率与采样位数较高的情况下,需要添加复杂的时序约束,才能保证每个乘累加器的y输入都接收到正确数据,而这实现起来是非常困难的,有时是不可能的。为了解决这个问题,参照对x输入流水化的方法,对y输入也进行流水化处理,改进为图2所示的并行流水结构。此结构在数据输入完毕后,各个乘累加器将依次输出相关结果,且在第一个乘累加器输出结果后,做相应的清零,就可以进行新数据的相关运算。