白点算法[2]依据这样的假设,即图像中颜色最浅的像素必定是白色或浅灰色。红色、绿色和蓝色通道最大值之间的差值提供的是与光源颜色有关的信息,校正的作用是进行色彩转换后让得到的颜色最大值完全相等。但是,要找出白点,就需要按亮度值对像素排序。另外可能还需要对排序后的列表进行时空滤波,抑制噪声伪影,最后将排序结果汇聚成唯一的白色三元色。使用白点法的优势是易于实现,缺陷则是会造成巨大的误差,可能导致原生场景的色彩掉色。另外这种方法的效果还容易被饱和像素削弱。
更加先进的方法是发挥色域转换的优势。这样色度可以轻易地与色彩饱和度和亮度隔离,将三维色彩校正问题降低为一维问题。
例如,先进行色彩饱和度映射,在YCC、YUV、L*a*b*或LuV色域中建立二维直方图,然后围绕直方图底部周边建立一个凸壳。计算出UV或(Cr,Cb)均值,用于校正色彩,让得到的色彩UV或CbCr直方图位于YUV、YCC、Luv或Lab域中的中性点或灰度点上。这些方法的优势在于能够得到更好的色彩表象,而缺陷则在于需要浮点算法才能实现。
所有上述的方法有一个共同的缺陷,就是如果曝光设置不当或者场景光照存在极度的动态范围,就会产生伪影。例如使用带原生色调的高亮光源照明,在图像中产生的饱和像素。典型如火焰位于焦点上的烛光照片,此时会导致完全饱和,图像上出现白色像素。
其它改善白平衡结果的方法
还有一种色彩校正方法就是将前景和背景分离。数码相机采用的自动对焦与矩阵测光相结合的方法,可以把镜头中心焦点周边的像素与靠近边缘的背景像素在空间上区分开来。这种方法假定拍摄的物体只有几种主要颜色,而且位于图像中心的焦点上。远处的物体靠近边缘,由灰度世界假设主导。
另一种方法围绕形状检测。面部或皮肤颜色检测有助于相机识别有预期色调的图像内容。这样只需要对有已知和预期的色调的像素进行白平衡校正。颜色校正就是将这些像素的颜色调整为贴近预期颜色。这种方法的不足之处就是分割和识别逻辑的成本不菲。大多数商业应用采用适应图像内容和拍摄环境的策略,综合应用多种方法[2] 。

用于相机校准和色彩校正的ISP
我们的实现方案采用如图3所示的典型图像传感器流水线技术。我们采用赛灵思基于可配置逻辑的图像处理内核来构建ISP的硬件部分(见蓝色方框)。同时,我们将相机校准和白平衡算法设计为运行在其中一个嵌入式ARM处理器上的C代码(见粉红色方框)。该ARM处理器还运行嵌入式Linux,为主机PC提供用户界面。
ISP中与白平衡和相机校准有关的部分是一个反馈环路,包括:
● 图像统计模块,用于逐帧采集各域的统计数据;
● 嵌入式驱动程序和应用软件,用于逐帧分析统计信息并对色彩校正模块编程;
● 色彩校正模块,用于逐像素地执行色彩转换。
我们将该ISP实现为Zynq视频和成像套件(ZVIK)1080x60相机图像处理参考设计的组成部分。
算法详解
为校准传感器的颜色,我们使用现成的颜色观察箱(X-Rite Macbeth Judge II)或灯箱。该设备有四个已知光谱的标准光源,分别用于模拟日光、冷白荧光灯、暖光荧光灯和白炽灯。我们还使用现成的色靶(X-Rite ColorChecker 24 色标准色卡),其色标具有已知的反射特性以及RGB与sRGB预期值。
在开始实现相机校准算法之前,我们首先将色靶放置在灯箱中,与灯箱的灰黑色背景平行。我们将色靶调整到一定位置,让来自所有光源的光照尽量均匀。
接下来,在打开所有光源的情况下,我们采集由传感器拍摄的有待校准的图像,此时尚未进行色彩校正(使用“跳过”色彩校正设置:将单位矩阵加载至色彩校正矩阵)。
然后使用赛灵思提供的MATLAB脚本协助补偿镜筒(几何形状)透镜畸变和镜头阴影(光强度在角落处下降)带来的影响。我们使用MATLAB脚本找出图像上的控制点,然后弯曲图像,用以对筒形畸变进行补偿。脚本的其余部分用于根据寄存的ColorChecker色靶背景来估算水平和垂直方向的光强度下降。
为衰减测量到的噪声,我们在色标中划出矩形区域。在这些区域中,我们计算出R、G、B像素数据均值,用RGB三元色表达每个色靶。带GUI的MATLAB脚本可帮助找出色标的中心,然后计算出与每个色标的RGB预期值(Re、Ge、Be)对应的平均RGB三元色。
我们采用模拟退火优化法找出色彩校正系数和偏移量。然后使用图3的色彩校正模块,将未经校正的(R、G、B)三元色转换为校正的(R’、G’、B’)三元色。
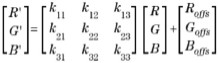
模拟退火算法的作用是求出一个能够返回标量的误差函数的最小值。在下面的讨论中,用Rk、Gk、Bk表示测得的色标像素值的子集或超集。用户可以自行限制包含在优化(子集)中的色标数量,也可多次使用某个特定的色标,以增大其在优化过程中的相对权重。整数n代表选优化的色标数量。如果一次优化全部色标,则对X-Rite ColorChecker 24 色标准色卡而言,n则为24。
因为优化算法最多只能设置12个变量(CCM系数和偏移量),一般来说不存在有能够将所有测量值精确映射到预期色标值的解决方案。不过该算法的目的是求出误差函数的最小值,从而在所使用的所有色标上实现理想的误差分布。